Введение
Модальной массой при сейсмическом воздействии в направлении dir (dir = OX, OY, OZ) называется величина
, где Гidir = (Mψi, Idir), M — матрица масс, ψi — собственный вектор (форма колебаний, отвечающая i-й частоте), Idir — вектор, компоненты которого равны 1, если соответствуют степени свободы сейсмического входа по направлению dir, и нулю в противном случае,
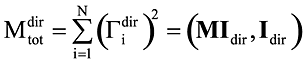
— общая масса, участвующая в движении по направлению dir.
Суммой модальных масс по направлению dir называется величина
, причем
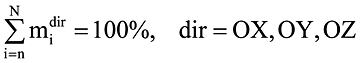
, где N — количество степеней свободы дискретной модели , n — количество удерживаемых собственных форм, n < < N.
В на примере простой задачи показана зависимость некоторых внутренних усилий от суммы модальных масс (рис. 1).
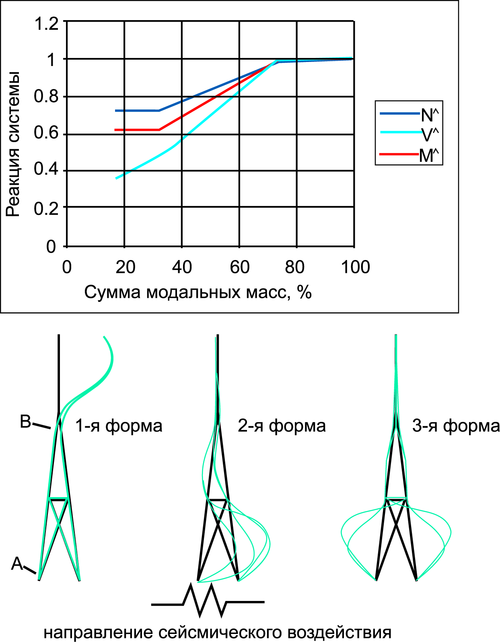
Рис. 1
Здесь NΛ = NA ⁄ NA100; VΛ = V ⁄ V100; MΛ = Mov ⁄ Mov100, NA — продольная сила в стержне А, V — суммарная сдвигающая сила в основании, Mov — опрокидывающий момент. Символ 100 означает, что этот фактор получен при удержании в решении всех собственных форм дискретной модели (100% модальных масс).
Рис. 1 иллюстрирует тот факт, что для получения достоверной сейсмической реакции сооружения необходимо удерживать такое количество собственных форм, чтобы обеспечить высокий процент модальных масс (не менее 80%). При этом, разумеется, расчетная модель должна достаточно достоверно описывать поведение системы.
Таким образом, сумма модальных масс в сейсмическом анализе используется как индикатор достаточного количества удерживаемых форм колебаний.
При решении ряда задач было обнаружено, что суммы модальных масс сходятся крайне неравномерно и очень медленно . При работе с расчетными моделями, содержащими большое количество степеней свободы (несколько сот тысяч), возникает серьезная проблема определения большого количества частот и форм собственных колебаний (порядка нескольких тысяч), представляющая собой сложную вычислительную задачу.
В этой работе представлен один из методов решения — блочный метод Ланцоша со сдвигами, реализованный автором в программном комплексе SCAD.
Архив записей
Архив записейВыберите месяц Апрель 2021 (1) Март 2021 (1) Сентябрь 2020 (1) Август 2020 (2) Июль 2020 (2) Июнь 2020 (2) Декабрь 2019 (3) Ноябрь 2019 (4) Октябрь 2019 (3) Сентябрь 2019 (2) Май 2019 (1) Октябрь 2018 (1) Июнь 2018 (1) Апрель 2018 (1) Январь 2018 (1) Ноябрь 2017 (1) Октябрь 2017 (1) Сентябрь 2017 (2) Август 2017 (4) Июль 2017 (5) Июнь 2017 (4) Май 2017 (5) Апрель 2017 (2) Март 2017 (1) Февраль 2017 (1) Январь 2017 (3) Декабрь 2016 (1) Ноябрь 2016 (2) Октябрь 2016 (3) Сентябрь 2016 (4) Август 2016 (6) Июль 2016 (9) Июнь 2016 (4) Май 2016 (5) Апрель 2016 (6) Март 2016 (5) Февраль 2016 (8) Январь 2016 (8) Декабрь 2015 (9) Ноябрь 2015 (4) Июль 2015 (1) Март 2015 (1) Февраль 2015 (1) Январь 2015 (1) Июль 2014 (1) Июль 2013 (1) Март 2013 (2) Декабрь 2012 (1) Ноябрь 2012 (1) Сентябрь 2012 (3) Август 2012 (4) Июль 2012 (4) Июнь 2012 (4) Май 2012 (4) Апрель 2012 (5) Март 2012 (7) Февраль 2012 (8) Январь 2012 (7) Декабрь 2011 (5) Ноябрь 2011 (1)
Выборка, генеральная совокупность и стандартное отклонение
Допустим, вы покупаете операционный усилитель (назовем его OPA100) и после некоторых экспериментов в лаборатории вы понимаете, что спецификации в техническом описании не дают вам достаточной информации о входном напряжении смещения при рабочих температурах вашего проекта. Чтобы исправить это, вы решили купить 15 операционных усилителей OPA100 (т.е. N = 15), провести измерения и сформировать статистику на основе этой выборки.
Если OPA100 имеет типовое напряжение смещения 1 мВ при соответствующей рабочей температуре, распределение напряжений смещения в 15-компонентной выборке может выглядеть примерно так:
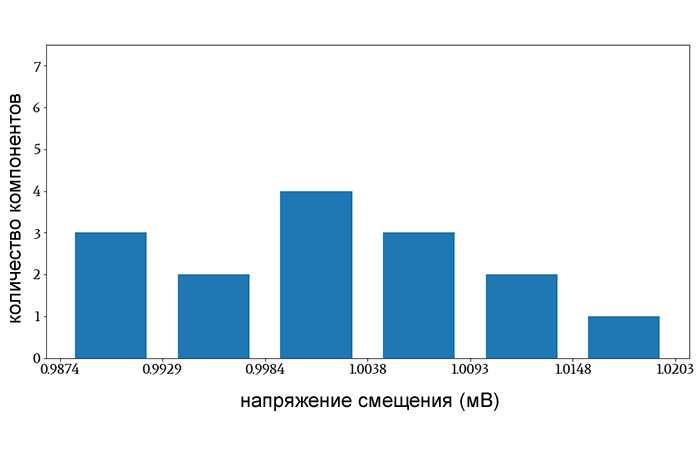 Рисунок 1 – По мере увеличения размера выборки измеренное распределение будет больше напоминать нормальное распределение.
Рисунок 1 – По мере увеличения размера выборки измеренное распределение будет больше напоминать нормальное распределение.
Вы измерили напряжение смещения каждого компонента, и теперь вы можете рассчитать стандартное отклонение, но сначала вам нужно задать себе вопрос: «я хочу рассчитать стандартное отклонение для выборки или для генеральной совокупности?». Другими словами, я должен отчитаться о стандартном отклонении этих 15 компонентов передо мной, или я должен попытаться отчитаться о стандартном отклонении, которое применяется ко всем операционным усилителям OPA100?
Стандартное отклонение выборки
Если мы работаем с выборкой и хотим знать стандартное отклонение выборки, мы делим на N. Это имеет смысл – как упоминалось выше, мы всегда делим на N при вычислении среднего арифметического, а стандартное отклонение включает в себя среднее арифметическое мощности отклонений в наборе данных.
Итак, чтобы продолжить наш пример, деление на N даст вам стандартное отклонение 15 операционных усилителей OPA100, которые вы приобрели.
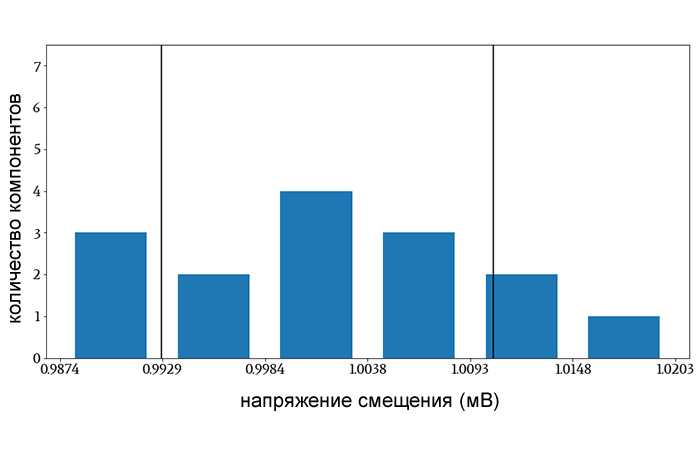 Рисунок 2 – Вертикальные линии показывают значения напряжения, которые на величину одного стандартного отклонения выше и ниже среднего значения выборки. При расчете стандартного отклонения я делил на N.
Рисунок 2 – Вертикальные линии показывают значения напряжения, которые на величину одного стандартного отклонения выше и ниже среднего значения выборки. При расчете стандартного отклонения я делил на N.
Другим типом данных, с которым часто сталкиваются инженеры-электронщики, является оцифрованный сигнал напряжения, и, как мы видели в предыдущей статье, стандартное отклонение представляет собой метод количественной оценки электрического шума.
Если вы хотите узнать стандартное отклонение полученного сигнала, то есть конкретные уровни напряжения, которые были оцифрованы и сохранены в памяти, и при расчете стандартного отклонения вы должны делить на N. В этом случае полученный сигнал является статистической выборкой.
Стандартное отклонение генеральной совокупности
Если мы работаем с выборкой и хотим знать стандартное отклонение генеральной совокупности, мы делим на N–1. Термин «генеральная совокупность» относится ко всей группе, для которой предоставленные данные дают репрезентативную выборку. Использование N–1 вместо N – это метод компенсации ошибки, связанной с конечным размером нашей выборки. Этот прием называется коррекцией Бесселя.
Коррекция необходима, потому что если мы хотим рассчитать стандартное отклонение генеральной совокупности, мы должны использовать среднее значение генеральной совокупности. Но обычно к генеральной совокупности у нас доступа нет. У нас есть только среднее значение выборки, которое является приблизительным значением среднего значения генеральной совокупности. Оказывается, что, когда мы используем среднее значение выборки вместо среднего значения генеральной совокупности, рассчитанное стандартное отклонение постоянно получается ниже реального, а деление на N–1 вместо N смягчает этот эффект.
Таким образом, если вы хотите оценить стандартное отклонение напряжения смещения для всех произведенных операционных усилителей OPA100, вам следует собрать данные из вашей 15-компонентной выборки, а затем при расчете стандартного отклонения делить на 14 вместо 15.
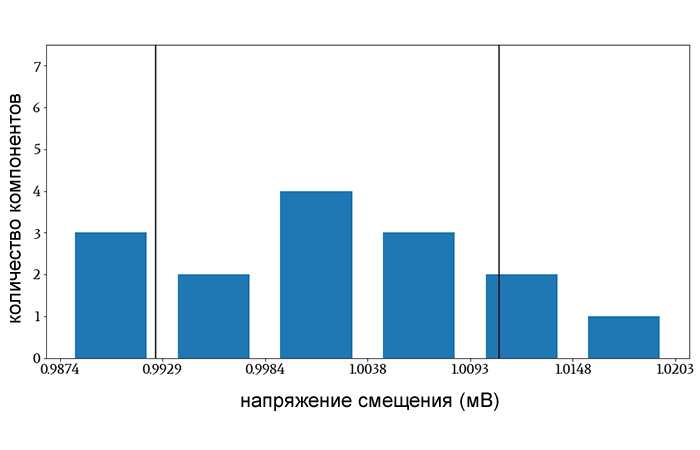 Рисунок 3 – Вертикальные линии показывают значения напряжения, которые на величину одного стандартного отклонения выше и ниже среднего значения выборки. При расчете стандартного отклонения я делил на N–1.
Рисунок 3 – Вертикальные линии показывают значения напряжения, которые на величину одного стандартного отклонения выше и ниже среднего значения выборки. При расчете стандартного отклонения я делил на N–1.
Точно так же, если вы хотите количественно оценить шум в напряжении сигнала на основе относительно короткого периода сбора данных, вы должны делить на N–1. В этом случае оцифрованные данные являются выборкой, а сам сигнал является генеральной совокупностью.
Вы также можете думать об этом следующим образом: когда мы делим на N–1, мы фокусируемся на основных процессах, которые создают шум в анализируемом сигнале, а не измеряем влияние этих процессов в течение отрезка времени, представленного полученными точками данных.
Межквартильный размах
В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.
Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».
коэффициент вариации
– это отношение стандартного отклонения к средней, выраженное в процентах:
И вот теперь совершенно без разницы, в д.е. мы считали:
или в тысячах д.е.:
Примечание: на практике часто считают именно через , но для оценки коэффициента вариации всей генеральной совокупности, конечно же, корректнее использовать исправленное стандартное отклонение .
В статистике существует следующий эмпирический ориентир:
– если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство вариант находится недалеко от средней, и найденное значение хорошо характеризует центральную тенденцию совокупности.
– если показатель вариации составляет существенно больше 30%, то выборка неоднородна, то есть, значительное количество вариант находятся далеко от , и выборочная средняя плохо характеризует типичную варианту. В таких случаях целесообразно рассмотреть , а иногда и перцентили, которые делят вариационный ряд на части, и для каждого участка рассчитать свои показатели. Но это уже немного дебри статистики.
Другое преимущество относительных показателей – это возможность сравнивать разнородные статистические совокупности. Например, множество слонов и множество хомячков. Совершенно понятно, что дисперсия веса слонов по отношению к дисперсии веса хомяков будет просто конской, и их сопоставление не имеет смысла. Но вот анализ коэффициентов вариации веса вполне осмыслен, и может статься, что у слонов он составляет 10%, а у хомячков 40% (пример, конечно, условный). Это говорит о сбалансированном питании и размеренной жизни слонов. А вот хомяки там, то носятся с голодухи по полям, то отъедаются и спят в норах, и поэтому среди них есть много худощавых и много упитанных особей ![]()
Кроме коэффициента вариации, существуют и другие относительные показатели, но в реальных студенческих работах они почти не встречаются, и поэтому я не буду их рассматривать в рамках данного курса.
И сейчас, конечно же, задачки для самостоятельного решения:
Пример 17, на отработку терминов и формул:
а) Стандартное отклонение выборочной совокупности равно 5, а средний квадрат её вариант – 250. Найти выборочную среднюю.
б) Определите среднее квадратическое отклонение, если известно, что средняя равна 260, а коэффициент вариации составляет 30%.
и Пример 18, творческий:
Производство стальных труб на предприятии (тонн) в 1-м полугодии составило:![]()
Определить:
– среднемесячный объем производства;
– среднее квадратическое отклонение;
– коэффициент вариации.
Сделать краткие содержательные выводы. – Да, это тоже типичный пункт статистической задачи!
Обратите внимание, что здесь не понятно, выборочной ли считать эту совокупность или генеральной. И в таких случаях лучше не заниматься домыслами, просто используем обозначения без подстрочных индексов
Вообще, задачи на экономическую и промышленную тематику – самые популярные в статистике, и в моей коллекции их сотни. Но все они до ужаса однотипны, и поэтому я предлагаю их в терапевтической дозировке ![]()
Задание 8
Выполнить расчёты в Экселе – числа уже там, ну а инструкцию я на этот раз не привёл, поскольку люди вы уже опытные.
Краткое решение и ответ в конце урока, который подошёл к концу.
Следующее занятие не за горами, а уже за кочкой:
Решения и ответы:
Пример 17. Решение:
а) Используем формулу . По условию, , . Таким образом:![]()
б) Используем формулу . По условию, , . Таким образом:
Ответ: а) , б)
Пример 18. Решение: вычислим сумму вариант и сумму их квадратов:Найдём среднюю: тонны – среднемесячный объем производства за полугодие.Дисперсию вычислим по формуле:![]() Среднее квадратическое отклонение: тонн.Коэффициент вариации:
Среднее квадратическое отклонение: тонн.Коэффициент вариации:
Ответ: тонны, тонн,
Краткие выводы: за первое полугодие среднемесячный объём производства труб составил тонны. Низкие показатели вариации говорят о стабильной ситуации на производстве.
(Переход на главную страницу)
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения
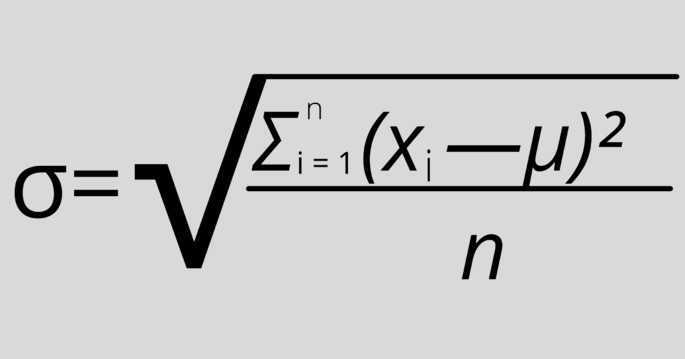 Где:
Где:
σ — стандартное отклонение,
xi — величина отдельного значения выборки,
μ — среднее арифметическое выборки,
n — размер выборки.
Эта формула применяется, когда анализируются все значения выборки.
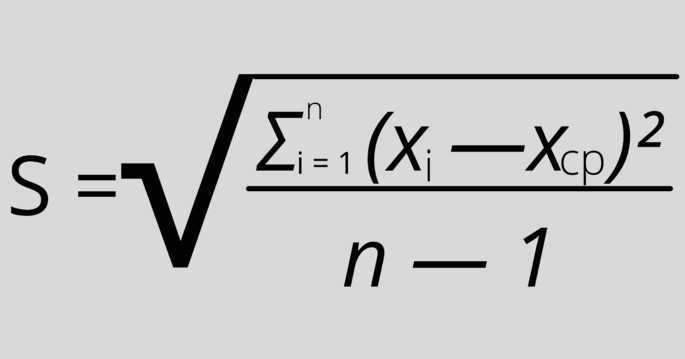 Где:
Где:
S — стандартное отклонение,
n — размер выборки,
xi — величина отдельного значения выборки,
xср — среднее арифметическое выборки.
Эта формула применяется, когда присутствует очень большой размер выборки, поэтому на анализ обычно берётся только её часть.
Единственная разница с предыдущей формулой: “n — 1” вместо “n”, и обозначение «xср» вместо «μ».
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
- только её часть – используется формула S (с «n–1»),
- полностью все данные – используется формула σ (с «n»).
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
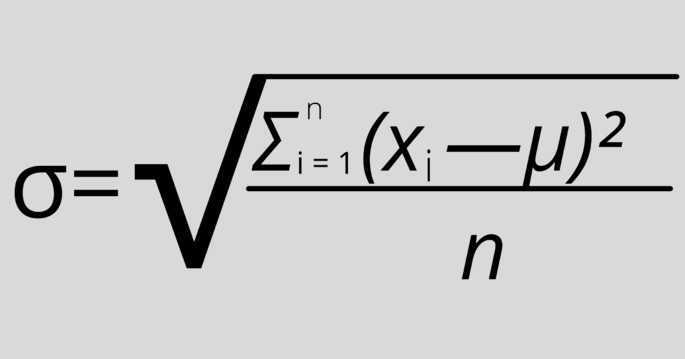
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
x1 — μ = 15 — 20 = -5
x2 — μ = 26 — 20 = 6
x3 — μ = 15 — 20 = -5
x4 — μ = 24 — 20 = 4
3. Каждую полученную разницу возвести в квадрат:
(x1 — μ)² = (-5)² = 25
(x2 — μ)² = 6² = 36
(x3 — μ)² = (-5)² = 25
(x4 — μ)² = 4² = 16
4. Сделать сумму полученных значений:
Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102
5. Поделить на размер выборки (т.е. на n):
(Σ (xi — μ)²)/n = 102 / 4 = 25,5
6. Найти квадратный корень:
√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
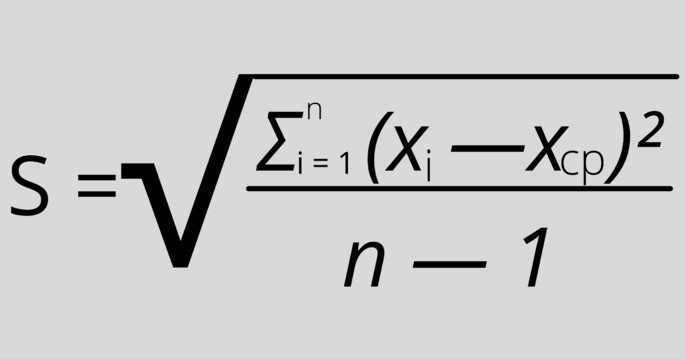
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
(X1 – Xср)² = (2,5)² = 6,25
(X2 – Xср)² = (–4,5)² = 20,25
(X3 – Xср)² = (–1,5)² = 2,25
(X4 – Xср)² = (–2,5)² = 6,25
(X5 – Xср)² = 5,5² = 30,25
(X6 – Xср)² = 0,5² = 0,25
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Образец отказограммы
В том случае, когда отказомера нет или он вышел из строя, в соответствии с п. 4.2. ТР 108-00 “Технические рекомендации по натурным испытаниям грунтов железобетонными сваями в условиях строительства” разрешается измерение остаточного отказа с прецизионного (высокоточного) нивелира. Для этого нивелир устанавливают на расстоянии 30-40 м от места забивки. При этом динамическое испытание сваи “под нивелир” оформляется соответствующим актом с обязательным указанием в нем типа и серийного номера нивелира, измеренной величины остаточного отказа сваи от конкретного числа ударов молота, даты забивки и номера испытываемой сваи. Акт подписывается геодезистами заказчика и генподрядчика, прорабом организации, выполняющей забивку свай, представителем испытательной лаборатории, а также представителем авторского надзора проектной организации.
Результаты испытания оформляют в журнале, форма которого приведена в ГОСТ 5686-2012 “Грунты. Методы полевых испытаний сваями” приложение Д.
После завершения добивки и определения отказов каждой пробной сваи результаты испытаний (журнал и отказограммы каждой сваи) направляются в проектную организацию, которая принимает окончательное решение о конструкции фундамента, расчетной нагрузке на сваи и необходимой глубине погружения их в грунт. При положительных результатах испытаний проектная организация дает разрешение на массовую забивку рабочих свай. Также в проектной документации должно быть указано, что нужно сделать с пробными (контрольными) сваями после проведения испытаний: удалить или срубить на определенной отметке.
Для того, чтобы возведение свайных конструкций было проведено на должном уровне, имело высокий уровень прочности, необходимо проводить испытания свай.
Компания «ПСК Основания и Фундаменты» предлагает статические и динамические виды испытания опорных конструкций. Динамическое испытание основывается на выявлении и тщательном просчете энергий ударов и несущих свойств опор.
В этой статье мы рассмотрим технологию, по которой принято производить испытания как специалистами ООО “Основания и Фундаменты”, так и всем, кто желает выполнить процедуру, не отклоняясь от норм.
Наши специалисты проведут испытания и определят несущую способность и возможные деформации свай.
Среднее линейное отклонение
Есть показатели вариации, которые учитывают сразу все значения, а не только отдельные наблюдения (типа максимума или минимума). Одним из таких является среднее линейное отклонение. Этот показатель характеризует меру разброса значений вокруг их среднего. В чем суть? Для того, чтобы показать меру разброса данных, нужно вначале определиться, относительно чего этот самый разброс будет считаться. Обычно это среднее арифметическое. Далее нужно посчитать, насколько каждое значение отклоняется от средней. Нас интересует среднее из таких отклонений. Однако напрямую складывать положительные и отрицательные отклонения нельзя, т.к. они взаимоуничтожатся и их сумма будет равна нулю. Поэтому все отклонения берутся по модулю. Средне линейное отклонение рассчитывается по формуле:
где
a – среднее линейное отклонение,
X – анализируемый показатель,
X̅ – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
Рассчитанное по этой формуле значение показывает среднее абсолютное отклонение от средней арифметической. Наглядная картинка в помощь.
Отклонения каждого наблюдения от среднего указаны маленькими стрелочками. Именно они берутся по модулю и суммируются. Потом все делится на количество значений.
Для полноты картины нужно привести еще и пример. Допустим, имеется фирма по производству черенков для лопат. Каждый черенок должен быть 1,5 метра длиной, но, что еще важней, все должны быть одинаковыми или, по крайней мере, плюс-минус 5 см. Однако нерадивые работники то 1,2 м отпилят, то 1,8 м. Дачники недовольны. Решил директор провести статистический анализ длины черенков. Отобрал 10 штук и замерил их длину, нашел среднюю и рассчитал среднее линейное отклонение. Средняя получилась как раз, что надо – 1,5 м. А вот среднее линейное отклонение вышло 0,16 м. Вот и получается, что каждый черенок длиннее или короче, чем нужно, в среднем на 16 см. Есть, о чем поговорить с работниками.
На этом сегодняшнюю заметку закончим. В следующей статье будут рассмотрены такие показатели вариации, как дисперсия, среднеквадратичное отклонение и коэффициент вариации.
Сравнение результатов численного моделирования и полевых испытаний методом Остерберга
На рисунке 6 сопоставлены графики зависимостисмещения от нагрузки, полученные при численном моделировании и подвергнутые обратному анализу, с графиками, полученными на основе измерений при полевых испытаниях сваи, построенной в 2012 году. Из этого рисунка видно, что конечноэлементная модель может вполне удовлетворительно описать поведение сваи при нагрузке с помощью ячейки Остерберга.

Рис. 6. Сопоставление зависимостей смещения от нагрузки при реальных и смоделированных испытаниях для двух направлений нагрузки (вверх и вниз) от О-ячейки на верхний и нижний испытываемые элементы сваи (по )
На рисунках 7–10 приведены кривые нагружения сваи (передачи нагрузки по ее длине) для четырех уровней нагрузки. Из этих рисунков хорошо видно, что результаты моделирования неплохо согласуются с фактическими. Разница между численными и измеренными данными становится совсем небольшой, когда уровень нагрузки увеличивается. Это, должно быть, связано с тем, что все параметры грунта определялись в соответствии с его поведением в предельно напряженном состоянии. Рисунки 7–10 показывают, что сопротивление дисперсного грунта по боковой поверхности верхней части сваи невелико, а основная часть нагрузки приходится на залегающие ниже слои скальных пород. При этом нагрузка, вызванная O-ячейкой, уменьшается вдоль сваи при удалении от ячейки. К оголовку сваи сила, направленнаявверх, уменьшается до нуля из-за компенсации отрицательной силой трения по боковой поверхности при взаимодействии сваи с грунтом (скальным и дисперсным). А с другой стороны сваи направленная вниз сила от воздействия О-ячейки уменьшается за счет компенсации положительной силой трения по боковой поверхности (аналогично механизму передачи нагрузки при традиционном испытании с использованием статической вдавливающей нагрузки на оголовок сваи).

Рис. 7. Сравнение кривых передачи нагрузки по длине сваи при реальных и смоделированных испытаниях методом Остерберга при нагрузке от О-ячейки 29,35 МН (по )

Рис. 8. Сравнение кривых передачи нагрузки по длине сваи при реальных и смоделированных испытаниях методом Остерберга при нагрузке от О-ячейки 62,90 МН (по )

Рис. 9. Сравнение кривых передачи нагрузки по длине сваи при реальных и смоделированных испытаниях методом Остерберга при нагрузке от О-ячейки 91,40 МН (по )

Рис. 10. Сравнение кривых передачи нагрузки по длине сваи при реальных и смоделированных испытаниях методом Остерберга при нагрузке от О-ячейки 120,25 МН (по )
На рисунке 11 сопоставлены кривые удельного сопротивления под нижним концом сваи в процессе смещения вниз ее нижнего испытываемого элемента (под О-ячейкой) по измеренным и численным данным. Близость этих кривых друг к другу указывает на то, что в PLAXIS можно удовлетворительно смоделировать полевые испытания, если имеется достаточная информация для определения параметров грунта. Следует отметить, что измеренная кривая является немного вогнутой. Возможно, это произошло из-за наличия некоторого количества осадков на дне скважины (как было указано в отчете по бурению, выполненному для устройства сваи) или из-за зависимости деформации от напряжения для песчаника с прослойкой сланца на уровне нижнего конца сваи. К сожалению, тонкий слой осадков в забое было трудно смоделировать методом конечных элементов из-за того, что если моделируется слой толщиной менее 10 см, то могут возникать численные ошибки.

Рис. 11. Сравнение усредненных кривых удельного сопротивления под нижним концом сваи в процессе его смещении вниз при реальных и смоделированных испытаниях методом Остерберга (по )
На рисунке 12 изображены кривые удельного сопротивления по боковой поверхности той части сваи, которая находится в скальной породе над силовой ячейкой. Видно, что измеренная и смоделированная кривые также приемлемо согласуются между собой. В любом случае приложенной нагрузке от О-ячейки сопротивлялась в основном часть сваи, находящаяся в скальной породе, благодаря высоким значениям параметров жесткости/прочности песчаника по сравнению с таковыми для дисперсного грунта.

Рис. 12. Сравнение усредненных кривых удельного сопротивления по боковой поверхности той части сваи, которая находится в скальной породе над силовой ячейкой (точнее, ее участка между высотными отметками 158,2 и 168 м) (по )
Показатели вариации
Вариация — это различие значений величин X у отдельных единиц статистической совокупности. Для изучения силы вариации рассчитывают следующие показатели вариации: , , , , , .
Размах вариации
Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:
Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.
Cреднее линейное отклонение
Cреднее линейное отклонение — это средний модуль отклонений значений X от среднего арифметического значения. Его можно рассчитывать по формуле средней арифметической простой — получим среднее линейное отклонение простое:
Если исходные данные X сгруппированы (имеются частоты f), то расчет среднего линейного отклонения выполняется по формуле средней арифметической взвешенной — получим среднее линейное отклонение взвешенное:
Линейный коэффициент вариации
Линейный коэффициент вариации — это отношение среднего линейного отклонение к средней арифметической:
С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.
Дисперсия
Дисперсия — это средний квадрат отклонений значений X от среднего арифметического значения. Дисперсию можно рассчитывать по формуле средней арифметической простой — получим дисперсию простую:
Если исходные данные X сгруппированы (имеются частоты f), то расчет дисперсии выполняется по формуле средней арифметической взвешенной — получим дисперсию взвешенную:
Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:
Если значения X — это , то для расчета дисперсии используют частную формулу дисперсии доли:
.
Cреднее квадратическое отклонение
Выше уже было рассказано о , которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:
Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:
Квадратический коэффициент вариации
Квадратический коэффициент вариации — это самый популярный относительный показатель вариации:
Критериальным значением квадратического коэффициента вариации V служит 0,333 или 33,3%, то есть если V меньше или равен 0,333 — вариация считает слабой, а если больше 0,333 — сильной. В случае сильной вариации изучаемая статистическая совокупность считается неоднородной, а средняя величина — нетипичной и ее нельзя использовать как обобщающий показатель этой совокупности.
Предыдущая лекция…Следующая лекция…
Примечание. Почему именно квадраты разностей?
Но почему при вычислении дисперсии мы берём именно квадраты разностей? Допустим при измерении какого-то параметра, вы получили следующий набор значений: 4; 4; -4; -4. Если мы просто сложим абсолютные отклонения от среднего (разности) между собой … отрицательные значения взаимно уничтожатся с положительными:
.
Получается, этот вариант бесполезен. Тогда, может, стоит попробовать абсолютные значения отклонений (то есть модули этих значений)?
.
На первый взгляд получается неплохо (полученная величина, кстати, называется средним абсолютным отклонением), но не во всех случаях. Попробуем другой пример. Пусть в результате измерения получился следующий набор значений: 7; 1; -6; -2. Тогда среднее абсолютное отклонение равно:
.
Вот это да! Снова получили результат 4, хотя разности имеют гораздо больший разброс.
А теперь посмотрим, что получится, если возвести разности в квадрат (и взять потом квадратный корень из их суммы).
Для первого примера получится:
.
Для второго примера получится:
.
Теперь – совсем другое дело! Среднеквадратическое отклонение получается тем большим, чем больший разброс имеют разности … к чему мы и стремились.
Фактически в данном методе использована та же идея, что и при вычислении расстояния между точками, только примененная иным способом.
И с математической точки зрения использование квадратов и квадратных корней дает больше пользы, чем мы могли бы получить на основании абсолютных значений отклонений, благодаря чему среднеквадратическое отклонение применимо и для других математических задач.
О том, как найти среднеквадратическое отклонение, вам рассказал репетитор по математике в Москве, Сергей Валерьевич
Пример расчета выборочной дисперсии и стандартного отклонения выборки.
После расчета геометрических и арифметических средних доходностей двух взаимных фондов в Примере (1) мы вычислили две меры дисперсии для этих фондов, размах и среднее абсолютное отклонение доходности (см. Пример расчета размаха и среднего абсолютного отклонения для оценки риска).
Теперь мы вычислим выборочную дисперсию и стандартное отклонение выборки для доходности тех же двух фондов.
|
Год |
Фонд Selected |
Фонд T. Rowe Price |
|---|---|---|
|
2008 |
-39.44% |
-35.75% |
|
2009 |
31.64 |
25.62 |
|
2010 |
12.53 |
15.15 |
|
2011 |
-4.35 |
-0.72 |
|
2012 |
12.82 |
17.25 |
На основании приведенных выше данных сделайте следующее:
- Рассчитайте выборочную дисперсию доходности для (A) SLASX и (B) PRFDX.
- Рассчитайте выборочное стандартное отклонение доходности для (A) SLASX и (B) PRFDX.
- Сравните дисперсию доходности, измеренную стандартным отклонением доходности и средним абсолютным отклонением доходности для каждого из двух фондов.
Решение для части 1:
Чтобы вычислить выборочную дисперсию, мы используем Формулу 13 (значения отклонений приведены в процентах).
А. SLASX:
1. Среднее значение выборки:
\( \overline R \) = (-39.44 + 31.64 + 12.53 — 4.35 +12.82)/ 5 =
13.20/5 = 2.64%.
2. Квадратичные отклонения от среднего значения:
(-39.44 — 2.64)2 = (-42.08)2 = 1,770.73
(31.64 — 2.64)2 = (29.00)2 = 841.00
(12.53 — 2.64)2 = (9.89)2 = 97.81
(-4.35 — 2.64)2 = (-6.99)2 = 48.86
(12.82 — 2.64)2 = (10.18)2 = 103.63
3. Сумма квадратов отклонений от среднего составляет:
1,770.73 + 841.00 + 97.81 + 48.86 + 103.63 = 2,862.03.
4. Разделим сумму квадратов отклонений от среднего на (n — 1):
2,862.03/(5 — 1) = 2,862.03/4 = 715.51
B. PRFDX:
1. Среднее значение выборки:
\( \overline R \) = (-35.75 + 25.62 + 15.15 — 0.72 + 17.25)/5 = 21.55/5 = 4.31%.
2. Квадратичные отклонения от среднего значения:
(-35.75 — 4.31)2 = (-40.06)2 = 1,604.80
(25.62 — 4.31)2 = (21.31)2 = 454.12
(15.15 — 4.31)2 = (10.84)2 = 117.51
(-0.72 — 4.31)2 = (-5.03)2 = 25.30
(17.25 — 4.31)2 = (12.94)2 = 167.44
3. Сумма квадратов отклонений от среднего составляет:
1,604.80 + 454.12 + 117.51 + 25.30 + 167.44 = 2,369.17.
4. Разделим сумму квадратов отклонений от среднего на (n — 1):
2,369.17/4 = 592.29
Решение для части 2:
Чтобы найти стандартное отклонение, мы берем положительный квадратный корень из дисперсии.
A. Для SLASX, s = \( \sqrt 715.51 \) = 26.7%.
B. Для PRFDX, s = \( \sqrt 592.29 \) = 24.3%.
Решение для части 3:
Таблица 21 суммирует результаты части 2 для стандартного отклонения и включает результаты для MAD из Примера расчета размаха и среднего абсолютного отклонения для оценки риска.
|
Фонд |
Стандартное |
Среднее |
|---|---|---|
|
SLASX |
26.7 |
19.6 |
|
PRFDX |
24.3 |
18.0 |
Обратите внимание, что среднее абсолютное отклонение меньше стандартного отклонения. Среднее абсолютное отклонение всегда будет меньше или равно стандартному отклонению, потому что стандартное отклонение придает больший вес большим отклонениям, чем маленьким (помните, что отклонения возводятся в квадрат)
Поскольку стандартное отклонение является мерой дисперсии относительно среднего арифметического, мы обычно представляем среднее арифметическое и стандартное отклонение вместе при анализе данных.
Когда мы имеем дело с данными, которые представляют собой временной ряд процентных изменений, представление геометрического среднего, представляющего собой сложную ставку скорости роста, также очень полезно.
В таблице 22 представлены исторические геометрические и арифметические средние доходности, а также историческое стандартное отклонение доходности для годовой и месячной доходности S&P 500.
Мы представляем эту статистику для номинальной (без поправки на инфляцию) доходности, чтобы мы могли наблюдать первоначальные величины доходности.
|
Ставка доходности |
Геометрическое |
Среднее |
Стандартное отклонение |
|---|---|---|---|
|
S&P 500 (Годовая) |
9.84 |
11.82 |
20.18 |
|
S&P 500 (Месячная) |
0.79 |
0.94 |
5.50 |



















